All About Carbon-14 Dating
- James Chen
- Jun 3, 2020
- 2 min read
To determine the age of some fossils, archeologists use a method called Carbon-14 Dating. It is something we often hear, but what is it, and how does it work?
What is Carbon-14?
The common and well-known type of carbon is carbon-12 (C12). It has 6 protons and 6 neutrons in its nucleus. However, a chemical element is defined only by its number of protons, so there are other types of carbons with different neutron numbers. These types are called the isotopes of carbon. Carbon-13 (C13) is incredibly unstable. Carbon-14 (C14), with 8 neutrons instead of 6, is created on Earth from nitrogen-14 (N14). Radiation from the sun constantly bombards N14 atoms, some of which change into C14. C14 is radioactive: after a period of time, a C14 atom will decay back to N14.
Carbon-14 in Living Organisms
Plants require a constant supply of carbon, and by doing so, it absorbs C14 as well as C12. The two isotopes of carbon exist with a fixed ratio on Earth. This means plants and animals also have this fixed ratio of carbons in their bodies. Any C14 that has decayed can be replaced by ingestion.
After An Organism Dies
After an organism dies, it no longer ingests carbon.C12 does not decay, but C14 does. Specifically, its half-life is roughly 5700 years. This means after 5700 years, there will be half the amount of C14 remaining in the dead organism. If the organism is preserved as fossil, the carbon isotopes are locked in the fossil. Since the ratio of C12 and C14 is fixed when the organism dies, and the amount of C12 does not change, by knowing the amount of C12 in a fossil let you know how much C14 there was at the moment of death. Now we can find the age of the fossil, only knowing the amount of C12 and C14!
Calculations & Details
To know the age by knowing the amount of carbon isotopes, we can build an equation. First, half of C14 decays over 5700 years, so knowing how many 5700 years is in the fossil age, we can know how many times the amount of C14 have been halved. And then, by multiplying the amount of C12 by the natural ratio, we can determine the amount of C14 in the fossil now. Let t be the age of the fossil (this is what we want to determine), Ac12 represent the amount of C12, Ac14 represent the amount of C14 when the fossil is discovered, and R be the natural ratio of C14 to C12. Then, we have the equation:

Of course, when we discover a fossil, R, Ac12, and Ac14 are known values. We want to find t, so we manipulate the equation to get t isolated:
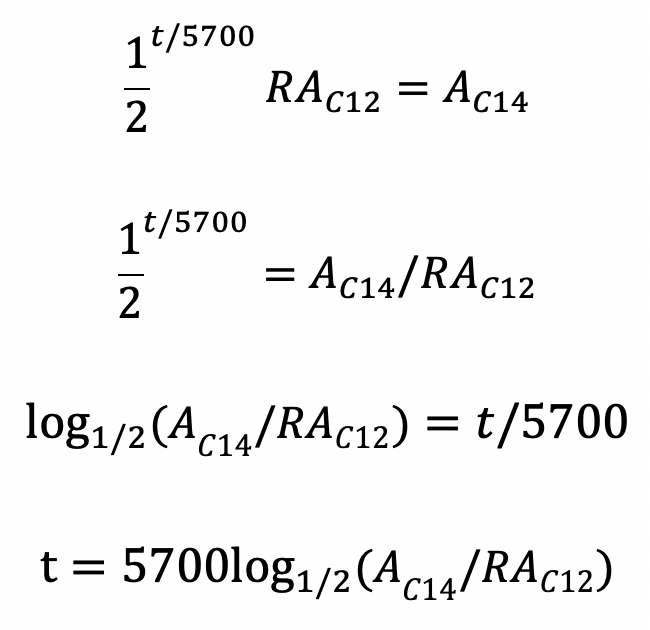
Now, by plugging in the values for R, Ac12, and Ac14, we can determine the age of the fossil.

Comments