Hawking Radiation: Calculating the Lifetime of a Black Hole
- Bryce Wong

- Jun 12, 2020
- 7 min read
Introduction:
I’m sure you’ve heard of the black hole. A vicious interstellar monster that is so mind-bogglingly massive that it relentlessly sucks up everything in their path with their immense gravitational pull. Not even light itself, the fastest thing in the universe, can escape. But black holes are not “invincible”. The famous theoretical physicist, Stephen Hawking, deduced that black holes have an intrinsic lifetime, dependent on the mass of the black hole – given an absurdly long time, due to quantum effects near the edge of the black hole, a black hole will actually evaporate into nothing!
Hawking radiation:
This evaporation of black holes is called Hawking radiation. A good way to think about is as follows (the actual process is a LOT more complicated!). In quantum mechanics, it is allowed for pairs of virtual photons to pop into existence spontaneously and move off in opposite directions. These pairs of photons then annihilate themselves shortly after. This all sounds “fine” for our daily lives; however, black holes are weird. Imagine what would happen at the event horizon (a black hole’s “boundary”). In the case of the event horizon, the black hole would be able to capture one of the photons, but the other photon would be able to escape off and fly infinitely far away – initially, it is just far enough to avoid black hole’s gravitational effects.
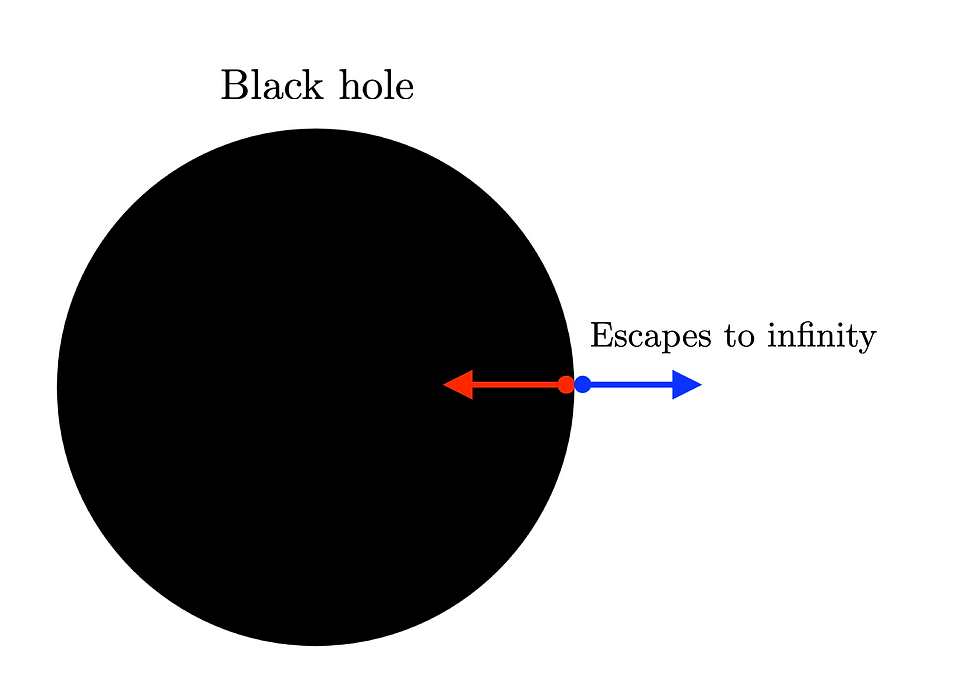
Now, the key realization is this: the escape of the photon suggests that this black hole is losing energy! Indeed, in some sense, the black hole is “glowing”, thereby losing energy via radiation. Since a black hole loses energy, it therefore must have a finite lifespan.
The beginnings of our calculation:
Needless to say, the physics used by Hawking to derive a formula for the lifetime of a black hole is incredibly, incredibly advanced. However, we can try our best to follow Hawking’s footsteps and use a few simple principles and cut a few corners to get a formula for a black hole’s lifetime that is frighteningly accurate. The method we will use is adapted from a talk given by UBC cosmologist Dr. Douglas Scott. The ingredients for our dish will be:
- the size of the black hole
- the Heisenberg uncertainty principle
- the mass-energy equivalence principle
- the average kinetic energy of particles in a system
- the rate an object radiates energy
We will see how these seemingly disparate principles all come together to result in our final calculation of the lifetime of a black hole.
The Schwarzschild radius:
Intuitively, we will need a way to quantify the size of a black hole in order to calculate the lifetime. This may seem like an impossible task – our current laws of physics break down in a black hole! But remember – we are interested in the effects that happen at the event horizon. The defining property of the event horizon is that it is the region where light itself begins to fall into the black hole. Therefore, we only need to use Newton’s laws of gravitation to find the event horizon’s distance away from the center of the black hole! And the key realization is that this is where the escape velocity is equal to the speed of light. Escape velocity is the minimum speed an object needs to escape infinitely far away from another object’s gravitational pull. By conservation of energy, the sum of the initial gravitational potential energy and the initial kinetic energy must be equal to the final energy of the object, which would be zero.
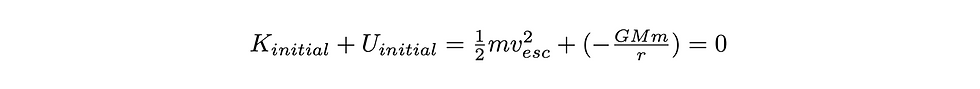
where m is the mass of the object, M is the mass of the black hole, G is Newton’s gravitational constant and r is the distance away from the black hole. Solving for the escape velocity yields
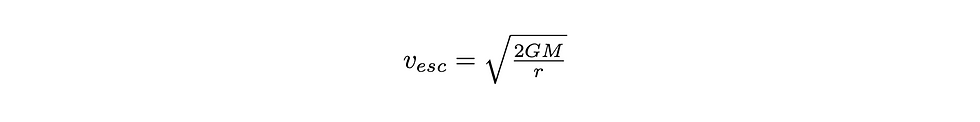
Note that this expression does not depend on the mass of the object – this is quite non-intuitive! Provided there is no air resistance, an extremely massive object will have the same escape velocity as an extremely light object! Now, all we simply need to do is set the escape velocity to the speed of light, c, and solve for r!
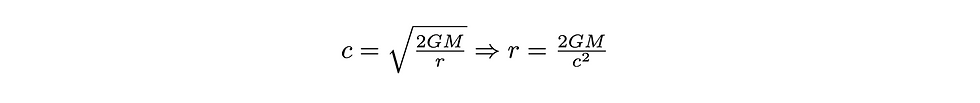
This quantity is known as the Schwarzschild radius – the radius of the event horizon of a black hole. If you ever venture below the Schwarzschild radius, you will never return. However, before we continue, I should give a warning. As we are doing astrophysics calculations, we must be true to the laws of astrophysics. That is, to simplify things, we will neglect all numerical factors. So, we will omit that “2” in the Schwarzschild radius in our further calculations.
The Heisenberg uncertainty principle:
Now that we have an expression for the size of a black hole, we need to somehow link this to energy. To do so, we can link the size of a black hole to the momentum of particles on the event horizon – it is fairly intuitive that there is a connection between momentum and energy. But do you know what is not intuitive? The Heisenberg uncertainty principle. This will be our link and it is a perfect example of how weird the quantum world is. The Heisenberg uncertainty principle states that for an object, the product of the object’s uncertainty in position and its uncertainty in momentum is at least as big as Planck’s constant divided by 4 pi.

This principle implies that no matter how accurate your equipment is, you will never be able to precisely measure something! But note that Planck’s constant is incredibly small, so in our daily lives, Heisenberg’s uncertainty principle is essentially invisible. For our black hole, we can use the uncertainty in position to calculate the uncertainty in momentum. Intuitively, let us say that the Schwarzschild radius is the uncertainty in position. Solving for the uncertainty in momentum and substituting while neglecting numerical factors yields
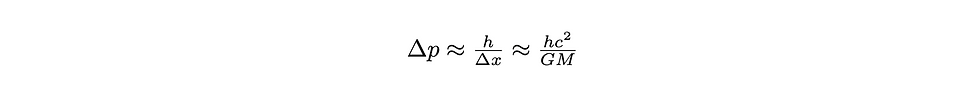
Now, the energy of a photon (or any other massless particle) is given by
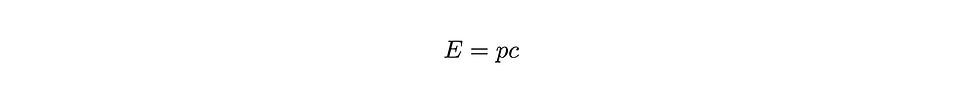
where p is the momentum of the particle. You might be thinking, “how can a massless particle have momentum?”. You can convince yourself of this by noting that a photon has energy – intuitively, there is a link between energy and momentum. For a hot gas of photons, it just so happens that uncertainty in energy is equal to the average energy of a photon (disregarding numerical factors). We can then substitute in our expression for the uncertainty in momentum and find the average energy per virtual photon at the event horizon:
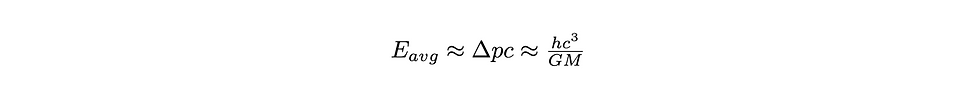
Temperature, energy, and the Stefan-Boltzmann law:
There is no such physical thing as “cold”. In reality, “cold” is simply the lack of “hot”. Since we know that the black hole is “glowing” and radiating energy, it is certainly worth investigating the temperature of a black hole. There is clearly a connection between energy and temperature (as temperature is a measure of the average kinetic energy of the particles in a system). Since we have an expression for the average energy per virtual photon, we should be able to calculate the temperature of the black hole. But first, we need a precise link between energy and temperature. For a gas, once again ignoring numerical factors, the energy per molecule of gas is directly proportional to temperature, multiplied by Boltzmann’s constant (we are approximating the virtual photons as a gas).

After substituting in our expression for the average energy per virtual photon, we can find the temperature of a black hole, known as the Hawking temperature.
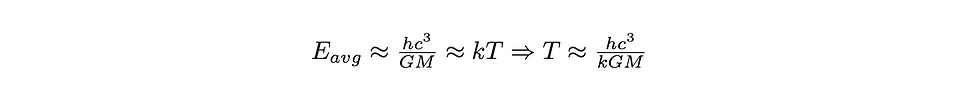
Now, we are nearly there, for we have the temperature of the black hole. Now we need the total energy of the black hole and an expression relating total energy, temperature, and lifetime. For the total energy of the black hole, we will use the most famous equation of all time:

This equation shows the equivalence between mass itself and energy itself: mass can be converted into energy and energy can be converted into mass! Now, a black hole will be slowly but surely losing mass, as it is radiating energy away. So, we can simply use this famous expression as the total energy of the black hole. All we need now is the final ingredient. If we can find the rate at which a black hole emits energy, we can complete our calculation! We can accomplish this by using the Stefan-Boltzmann law:
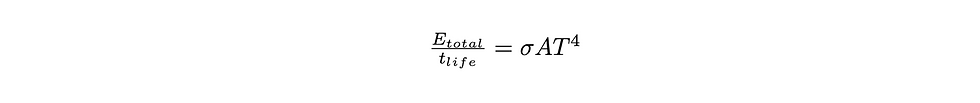
where T is temperature, A is the surface area of the object, and sigma is the Stefan-Boltzmann constant. Note that when we use the Stefan-Boltzmann law, we are assuming that the black hole is a perfect emitter. We substitute in the surface area (ignoring numerical factors) and the total energy of the black hole, and we find an expression for the lifetime (an incomplete expression, as we want the lifetime as a function of mass).
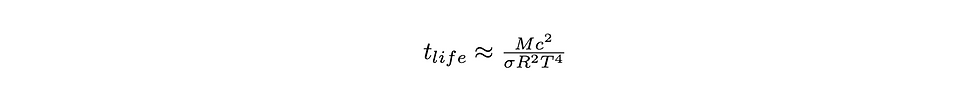
We substitute in the Schwarzschild radius and our expression for temperature:
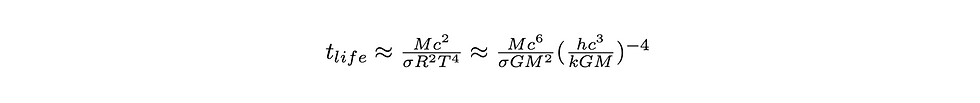
Simplifying, we arrive at our final answer – the lifetime of a black hole:

Whew!
Putting things into context:
First, we can see that the lifetime is proportional to the cube of the mass of the black hole! This means that for a moderate increase in the mass, the lifetime will increase a large amount. Moreover, before we do any numerical calculations, notice that Planck’s constant, raised to the 4th power, is in the denominator. For relevant values of M, the lifetime will be absolutely humongous. Let’s do a calculation. Say that the black hole has the mass of the sun. Now, let’s plug this into our lifetime equation, as well as all the constants.
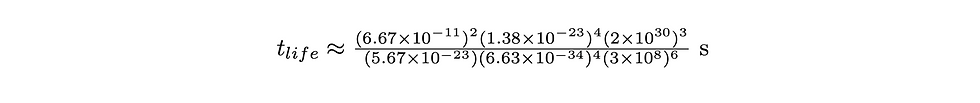
Whipping out our trusty calculator and converting this value into years gives
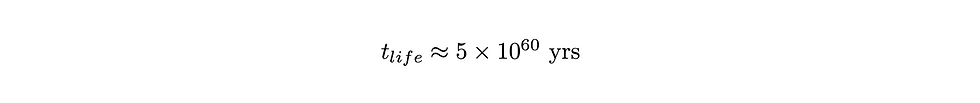
This is a colossal lifetime. It’s many, many orders of magnitude larger than even the age of the universe! And this is only for a black hole with the mass of the sun. There are black holes far more massive. For example, the famous black hole M87 is billions of times more massive than our sun. It is likely that when all the stars in the universe have burned out, and the universe is dark, supermassive black holes will be the final remnants of the world we live in, until even they evaporate.


Comments